| Kinderen gaan rekenen | deel: |
BEGINNENDE GECIJFERDHEID; TUSSENDOELEN EN INTERVENTIES
Ordenend handelen
Oriëntatie in ruimte en lichaam
Oriëntatie in de tijd
Meten en meetkunde
Tellen
Bewerkingen
Cijferkennis
Deelgebied 7. Cijferkennis
Tussendoelen
Klas 1 en 2
- De kinderen gebruiken verschillende symbolen waarmee zij getallen noteren.
- In klas 1 kunnen de leerlingen de getallen tot ca. 24 schrijven, verstaan en lezen. In klas 2 - in gewone cijfers - uitbreidend tot getallen bestaand uit cijfers voor eenheden, tientallen en honderdtallen.
- De kinderen kunnen getallen betekenis geven in contexten en positioneren op de rekenlijn (de lege getallenlijn).
- Kinderen kunnen een hoeveelheid verdelen.
- Onderdelen van deze tussendoelen:
- (her)kennen van de symbolen van 0-9
- (her) kennen van de getallen boven de 10
- Positiewaarde van de getallen kunnen lezen en schrijven
7.1 Uitleg
Cijfers en getallen kunnen verwijzen naar verschillende inhouden. Een kind staat aan de hand van moeder bij de bushalte terwijl deze aan een voorbijganger vraagt welke bus naar Wageningen gaat. Lijn 514 zegt de man. Hij kijkt naar zijn moeder en zegt: ’Dat is heel ver, Wageningen hè mama!’
Getallen en cijfers duiden verschillende zaken aan: aantal: twintig blokken in de mand telgetal: de zesde in de rij van twintig kinderen; nummer zes in de kring meetgetal: de leeftijd van vijf jaar naamgetal: buslijn 50 naar Wageningen rekengetal: tien is acht plus twee
Bij welke activiteiten werken we aan dit tussendoel?
7.2 Kleuterklas
In de meeste kleuterklassen komen de cijfers nog niet in beeld. Toch kennen veel kinderen de symbolen al. ‘Op mijn t-shirt staat een drie, maar ik ben vijf en ik woon op twintig’, vertelde een jongetje trots aan zijn juf, terwijl hij aan het tekenen was. Hij schreef precies de getallen voor haar op. In deze klas waren de symbolen niet zichtbaar aanwezig; dit kind had het ergens anders al geleerd. Het kan ook anders. Zonder expliciet les te geven over de cijfers en letters, kan een kleuterjuf ook besluiten om de symbolen al wel in de klassenomgeving op te nemen. In sommige kleuterklassen zijn houten cijfers aanwezig waar kinderen mee kunnen spelen. Dan hebben de hutten soms een huisnummer, of trekken kinderen de cijfers om of tekenen ze na. Het is grappig om te zien dat de kinderen die er nog niet aan toe zijn om de symboolwaarde te begrijpen deze cijferblokken gewoon als mooie blokvorm gebruiken bij hun spel, terwijl er ook al kinderen zijn die de waarde van de getallen koppelen aan het beeld. Die willen bijvoorbeeld het blok dat ‘net zo oud is’ of het blok ‘dat het meeste’ is.
Een voorbeeld uit een klas waar de juffen doelbewust wel de cijfers en letters willen integreren in het vrije spel. In de klas hangt een cijfer- en letterkaart zoals ze die ook in de eerste klas krijgen. Niet met doel te oefenen, maar we zien dit als een mogelijkheid voor kleuters die dat willen, om te gaan schrijven en sommetjes maken. Ieder jaar is er wel een periode is in de kleuterklas dat kinderen met elkaar sommetjes gaan maken. Niet alleen oudste kleuters doen daar aan mee. Hele bladen worden dan volgeschreven. ‘Weet jij....?’ (vragen ze aan elkaar), ‘kan jij deze al ?’ enz. Pieter, met een achterstand in de fijne motoriek maar wel al zeseneenhalf jaar oud, kan behoorlijk goed hoofdrekenen. Hij kan alleen nauwelijks de cijfers schrijven. Geconcentreerd, tong uit de mond maakt hij sommen voor anderen, hij kijkt steeds op de cijferkaart en is zeer tevreden met het resultaat. Hij geeft de sommen aan Marieke van bijna zes. Zij zegt: ‘Maar ik kan het niet lezen’. ‘Nee’, zegt Pieter stralend, ‘het zijn ook geheime sommen!’ Ze giechelen en gaan ze samen maken....
7.3 Eerste klas en tweede klas
Cijferkennis, plaatswaarde en positioneren
7.3.1 Cijferkennis
Als de kinderen in de onderbouw komen worden aan al de getalservaringen die in de kleuterklas zijn opgedaan namen en symbolen verbonden. In eerste instantie worden de hoeveelheden nog weergegeven als Romeinse cijfers of middels het turven. Hier is de directe link met hoeveelheden nog direct te leggen. Via synchroon tellen of gestructureerd tellen geven de kinderen het weergegeven aantal weer. De stap daarna komt los te staan van de hoeveelheid. De Arabische cijfers doen hun intrede.
Aan het correct leren schrijven van de cijfers zou op dezelfde manier veel aandacht moeten worden besteed als aan het leren schrijven van de letters. Het duurt vaak nog tot ruim in de tweede klas, voordat de schrijfwijze correct geautomatiseerd is. Zo lang zouden leraren alert moeten blijven op kinderen die de schrijfrichting niet beheersen en bijvoorbeeld opeens de negen van beneden naar boven tekenen. Het is raadzaam om in een schrijfmethode te kijken hoe het schrijven van de cijfers op zich wordt aangelegd. En net zo als bij de letters de klank-teken koppeling tot stand moet komen, zo moet bij de cijfers de ‘waarde-symbool’ koppeling tot stand komen. De eerste tijd in de eerste klas, zal er ook veel aandacht uitgaan naar het tot stand komen van deze vaardigheden.
![]()
• Voorbeelden hoe gewerkt kan worden aan het vergroten en automatiseren van de cijferkennis:
Het verbinden van een betekenis aan de cijfers. Kinderen hebben kastanjes verdeeld en tekenen de manier waarop de kastanjes verdeeld zijn. De leraar vraagt of ze de aantallen er in cijfers bij willen zetten. Lezend en schrijvend leren de kinderen de cijfers kennen. De werkvormen zijn legio en voor de hand liggend: wat staat hier? Schrijf op ‘zeven’, zet een rondje om iedere 8 enz. Maar bij het geven van een getaldictee kunnen meerdere vaardigheden tegelijkertijd worden geoefend, bijvoorbeeld wanneer een leraar vraagt ‘hoeveel keer tik ik tegen het bord?’ en de kinderen dat vervolgens in cijfers op moeten schrijven. Het verschil met het klassieke dictee (schrijf op 7) is, dat de kinderen nu naar het telgetal wordt gevraagd. Zo kan in een simpel cijferdictee afwisselend gevraagd worden naar aantal (schrijf op hoeveel lampen er in de klas zijn) meetgetal (schrijf op welke schoenmaat je hebt), naamgetal (schrijf op in welke klas we zitten), telgetal (schrijf op hoe vaak ik gesprongen heb). In de tweede klas wordt dit uitgebreid naar het gebied tot honderd en wellicht verder. Ook leesactiviteiten kunnen worden ingevoegd; een flitskaartje laten zien, een getal opschrijven en in aantallen stipjes laten weergeven enz.
• Nog een paar ideeën: Op de rug wordt een getal geschreven. Het kind schrijft vervolgens het getal op papier.
Dobbelstenen: een kind gooit, de ander schrijft op (n.b. maak gebruik van minimaal 2 dobbelstenen). Dobbelstenen: Om de beurt gooien twee kinderen met een dobbelsteen en ze schrijven op en tellen door (n.b. bij het passeren van een afgesproken getal ‘omdraaien, dus aftrekken wat er wordt gegooid).
Memoriespel. Een leraar of een kind uit een hogere klas maakt kaartjes met een beeld van turven en een van het cijferbeeld. Wanneer eerst de Romeinse cijfers zijn gebruikt, dan een kaartje met een beeld van het Romeinse cijfer en een kaartje met het beeld van het cijfer.

Flitskaarten Maak flitskaarten van dobbelsteenpatronen (enkele dobbelstenen om de patronen te herkennen, dubbele dobbelstenen om de bewerkingen mee te oefenen); Op deze manier helpen we de kinderen met het herkennen van patronen en aantallen. Ook bewerkingen kunnen geoefend worden: een gegooide 4 en 6 is samen 10. Flitskaarten kunnen ook gebruikt worden om de cijfersymbolen op zich te herkennen:
-ik draai een kaartje snel om en jullie schrijven het getal op het papier -ik draai een kaartje snel om en jullie turven het aantal op papier -ik draai een kaartje snel om en jullie laten het aantal klappen horen dat erbij hoort
Met dominostenen gemaakt in cijfers of in combinatie met cijfers en aantallen getekend kunnen kinderen ook de waarde van de cijfers leren.
Bordspelen Alle bordspelen uitgevoerd met dobbelstenen waar de cijfers op geschreven staan in plaats van de dobbelsteenpatronen. Of bordspelen waarbij op het speelbord een rij getallen wordt bewandeld, bijvoorbeeld ganzenbord met op ieder vakje een nummer. Kinderen maken dit soort bordspelen ook graag zelf.
Koppelen van het cijfer aan de hoeveelheid:
- Laat kinderen tekeningen maken waarin de 5 te tellen is. Bijvoorbeeld een hoed met vijf punten, de hemel met vijf grote sterren.
- Laat in zand, op het bord of op de grond de 5 vijf keer opschrijven.
- Hoeveel knikkers heb ik in mijn hand? Schrijf eens op.
- Een kind heeft een knikkerzak en pakt daar knikkers uit in een gesloten vuist. Anderen raden hoeveel dat er zijn.
- In tijdschriften zoeken naar verschillende vijven (allerlei vormen waarin de vijf geschreven kan worden en de kinderen daar aan collage van laten maken)
- Een voelzak laten maken waarin allerlei voorwerpen gevoeld kunnen worden. Bijvoorbeeld in een zak zitten allerlei voorwerpen maar er zitten ook vijf glazen knikkers in. De kinderen krijgen de opdracht te voelen naar de voorwerpen waar er meer van zijn en die aantallen op te schrijven.
- Verschillende soorten getallenlijnen op hangen. Met kralen in 10-structuur, met stippen, met strepen met en zonder cijfers.
- Rara platen. Maak zelf een boek waar op elke bladzijde een aantal te vinden is. Bijvoorbeeld op bladzijde 3 zien we drie eenden (natuurlijk is er meer te zien, maar van een ding zijn er drie, in dit geval eenden); op bladzijde 4 vier deuren enz.
- Van allerlei materialen de cijfers maken. Schuurpapier, scheuren, plakken enz.
Kwaliteit van de getallen Wanneer kinderen zich buigen over vragen als ‘Waar zijn er vier van in de wereld?’ of ‘Wat hoort er voor jou bij de 4?’, worden getal, cijfer en waarde geïntegreerd. De vier windrichtingen, de adventskaarsen, de wielen van een auto en het broertje van Johan dat vier jaar is en bij juffie Rikkie in de klas zit, worden allemaal weergegeven door hetzelfde symbool. ‘Wat kan je toch veel schrijven, met een zo’n letter, zei een eerste klasser eens. Hij had natuurlijk gelijk, want we kunnen de hele wereld (waarvan is er maar 1?) aangeven met maar één enkele streep.
Telboekjes maken. Bijvoorbeeld het telboekje van de 4. Daarin wordt de 4 geschreven, geturfd, getekend op allerlei manieren.
Aan de lijn hangen de getallen 0 t/m 10 en later is dit natuurlijk uit te breiden. Welk cijfer komt na de …….? Waar moet…… hangen?
Welk cijfer ontbreekt? Een aantal voorbeelden. Deze rij is natuurlijk uit te breiden tot de twintig en in de tweede klas tot de 100. Dan ontstaan er meerdere mogelijkheden (zie positioneren op de getallenlijn)

Welke cijfers ontbreken in deze rij?

Vul de cijfers eens in.

Welke cijfers hangen verkeerd? Hang ze eens goed op.
 Welke getallen zitten er tussen de 3 en 7? Wat komt er na de 7? Wat komt er voor de 3?
Welke getallen zitten er tussen de 3 en 7? Wat komt er na de 7? Wat komt er voor de 3?

Welke getallen moet ik nu nog weghalen om het rijtje af te maken?
7.3.2 De plaatswaarde van de getallen
Waar staan de honderdtallen, tientallen en eenheden.
Voorbeeld 1
Een materiaal wat een goed beeld geeft van deze plaatswaarde is het MAB materiaal. Kinderen kunnen getallen leggen met de 100-schijf, de 10-staaf en de losse kleine blokjes. Er ontstaat een duidelijke opbouw van het getal . Kinderen kunnen op deze manieren getallen leggen en krijgen een beeld van de opbouw.

Voorbeeld 2
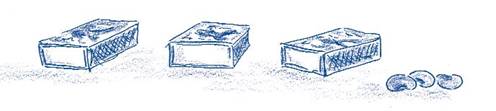
Opbergen van materiaal. Alle kinderen van een groepje halen de bonen er uit en gaan ze ‘opbergen’ In elk luciferdoosje mogen 10 bonen opgeborgen worden. De bonen die over zijn worden er los naast gelegd. Schrijf op hoeveel bonen er zijn.
Voorbeeld 3
Laat kinderen naar een getal springen met sprongen van 10 en 1 Spreek daarbij af dat bijvoorbeeld een tiental een sprong is en dat een eenheid een stap is. Schrijf op hoeveel er gesprongen en gelopen is.
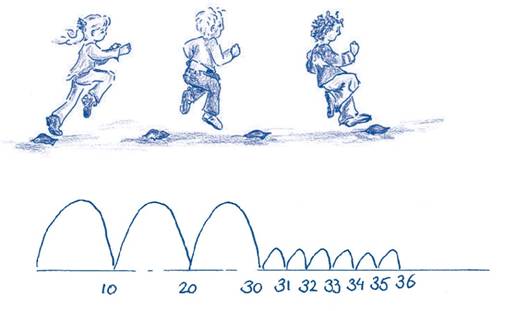
Voorbeeld 4
Op een getallenlijn met de grote telrij staan de getallen 10 t/m 100 aangegeven. We laten kinderen allerlei opdrachten uitvoeren van het plaatsen op de getallenlijn.
- welke getallen zitten er tussen de 20 en 30?
- Wat ligt er precies tussen de 70 en 80
- Aan een lijn hangen de getallen van de grote telrij. De kaartjes die meester uitdeelt moeten op de goede plaats worden gehangen.
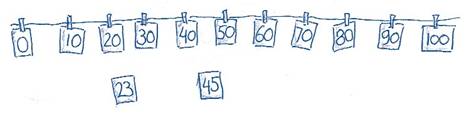
Sommige kinderen hebben baat bij het duidelijk scheiden van de honderdtallen, tientallen en eenheden

Voorbeeld 5
Inschatten van de afstand tussen getallen Welk getal ligt dichter bij de 50: 43 of 47? Welk getal ligt dichter bij de 50: 43 of 54? Wat ligt er precies tussen 50 en 60? Wat ligt er precies tussen 23 en 33?
De wijze waarop getallen worden geschreven. Veel kinderen houden moeite met schrijven van de getallen boven de tien. 63 wordt vaak geschreven als 36. Door met stroken gekleurd papier te werken, kunnen kinderen die hiermee moeite houden makkelijker zien wat de waarde is van ieder cijfer; in de rode baan de honderdtallen in de blauwe baan de tientallen en de eenheden er los naast. Veel rekenproblemen in hogere klassen komen voort uit deze verwarring. Wanneer kinderen bewerkingen gaan uitvoeren door te cijferen, mogen ze zich niet meer vergissen in de juiste schrijfwijze en positionering van de getallen, anders komt de som niet uit. In de eerste en tweede klas moet hier dus veel aandacht aan worden besteed. Veel kinderen houden ervan om dit te oefenen op lange stroken papier waarop de getallen onder elkaar worden opgeschreven (kassabonnen). Gedurende een rekenperiode iedere dag een kassabon laten schrijven vanaf een ander begingetal (bijvoorbeeld vandaag een kassabon die begint op de 12, jullie hebben 5 minuten de tijd, kijk maar hoever je komt) geeft de kinderen in korte tijd veel oefening op dit gebied. Soms worden deze kassabonnen aan het begin vastgeplakt en dan opgerold rond een saté stokje om zo een aansprekend oefenstrookje te creëren.
Maar ook is het voor kinderen niet vanzelfsprekend om lezend te zien wat meer is 24 of
21. Dat komt omdat er zoveel verschillende handelingen moeten worden uitgevoerd: eerst moet het getal gelezen worden, dan moet een kind zich realiseren hoeveel het is en dan moeten de beide getallen met elkaar worden vergeleken. Het lijkt voor volwassenen zo simpel, maar kinderen hebben tijd en oefening nodig om dit te leren.
Voorbeeld 1
Twee getallen op het bord: Wat is meer? Wat komt ervoor? Komt (leraar noemt een ander getal) ervoor of erna? Zet ze eens in volgorde (open getallenlijn). Komt de 17 voor of na de 16 of op de getallenlijn tot 100?
Komt de 45 voor of na de 54? Kinderen die hiermee moeite houden, weten vaak wel dat 50 meer is dan 40. Ook dat 40 dus eerder op de getallenlijn geplaatst wordt dan 50. Zij kunnen baat hebben bij een getallenlijn in de klas waarbij ieder tiental een eigen kleur heeft. Als nu 54 in dezelfde kleur is als 50 en 45 hoort bij de kleur van de 40, dan kan dat helpen om deze vraag te beantwoorden.
7.3.3 Positioneren op de getallenlijn
In eerste instantie is het raadzaam om te beginnen met de kralensnoeren uit de rekenkist. Deze oefeningen kunnen worden uitgevoerd met het 20-snoer en het 100-snoer.
Voorbeeld 1
Voorbeelden van opdrachten aan de kinderen
‘Schuif 12 kralen weg en zet een wasknijper tussen.’ ‘Doe hetzelfde met een volgende wasknijper nog een keer.’ ‘Waar is de 35ste kraal?’ ‘Zet de wasknijper na de 24ste kraal.’ Houd een strook papier voor de snoer. Hoeveel kralen zitten hier achter verborgen?
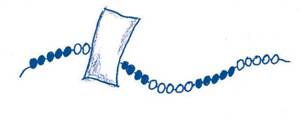
Ditzelfde kan worden gedaan met een afbeelding van het 20- en/of 100-snoer
Voorbeeld 2
Maak met de kinderen een getallensnoer. De kinderen hebben ronde kartonnen met daarop de getallen van 1 tot en met 20. Zij verbeelden de kralen. Een kind zet hen in de goede volgorde. De leraar helpt bij het begin. Hier is de 1daar is de 20. Iedereen denkt mee: Waar zou de 10 moeten staan? En de5? Wie komt er na de 5 en zie voor de 5? Wie vlak voor de 20? Wie denken jullie dat er allemaal na de 20 komen?
voorbeeld 3
Dezelfde oefening kan met een getallenlijn met 20 lege vakjes op het bord, of op een eigen papier worden gemaakt. Maar dezelfde oefening kan ook met de helemaal lege getallenlijn worden gemaakt. Als voorbeeld de lege lijn tot 100. Dan kan de leraar vragen stellen en opdrachten geven. Waar is de 50? Teken hem eens in. En de 25 dan? Waar zou de 30 liggen. Kun je me vertellen hoe je daar achter ben gekomen? Waar ligt de 5? Zou je boogjes van 5-sprongen naar de 30 kunnen tekenen?